空間という語は、建築分野と数学（幾何学）分野の双方で用いられる。しかし両者が同じものを指しているかというと、必ずしもそうではない。
本稿の目的は、この不整合を用語の誤用や理解不足として片づけるのではなく、分野ごとに空間という語が何を中心に据えて使われているのかという観点から整理することにある。¹

建築の実務者が幾何学に触れるとき、あるいは数学的な説明を読むとき、この違いを意識していないと議論が噛み合わない場面が生じることがある。以下では、必要最小限の前提にとどめつつ、建築と数学それぞれにおける空間の意味を対比的に示す。

建築における空間：経験としての空間

建築の文脈で空間と言うとき、それは一般に、壁・床・天井・間仕切りなどによって囲われたり、区切られたりした範囲を指す。²囲われた範囲を内部空間、その外側に広がる周囲の範囲を外部空間と呼んでも差し支えない。

このような空間の重要な特徴は、人が移動し、滞在し、行為できるという点にある。これは、壁の内部や床の中といった固体の領域では同じことができない点と対照的である。

建築の空間は、木材やコンクリート、ガラスといった物質的な要素があって初めて成立する。しかし、空間そのものは物質ではない。空間は、人に認識され、他者と共有される経験のまとまりとしての概念である。³
言い換えれば、建築における空間とは、物質によって支えられてはいるが、物質そのものとは異なる水準で立ち上がる対象である。

幾何学における空間：構造としての空間

一方、幾何学を含む数学の文脈で空間と言うとき、それはまったく異なる意味をもつ。

例えば、水は H₂O分子の集合体である。ここで水が液体としてまとまるのは、分子がただ集まっているからだけではなく、水素結合などの分子間力によって、分子どうしの結びつきが生まれているからでもある。
これと同様に、数学における空間も、まず要素の集合があり、そこに距離や近傍といった規則を与えることで、要素どうしの関係（近い・つながる・連続に変化するなど）を扱えるようになる。⁴ただし数学で扱う要素は物質的な粒子ではなく、あくまで抽象的な要素によって構成される。

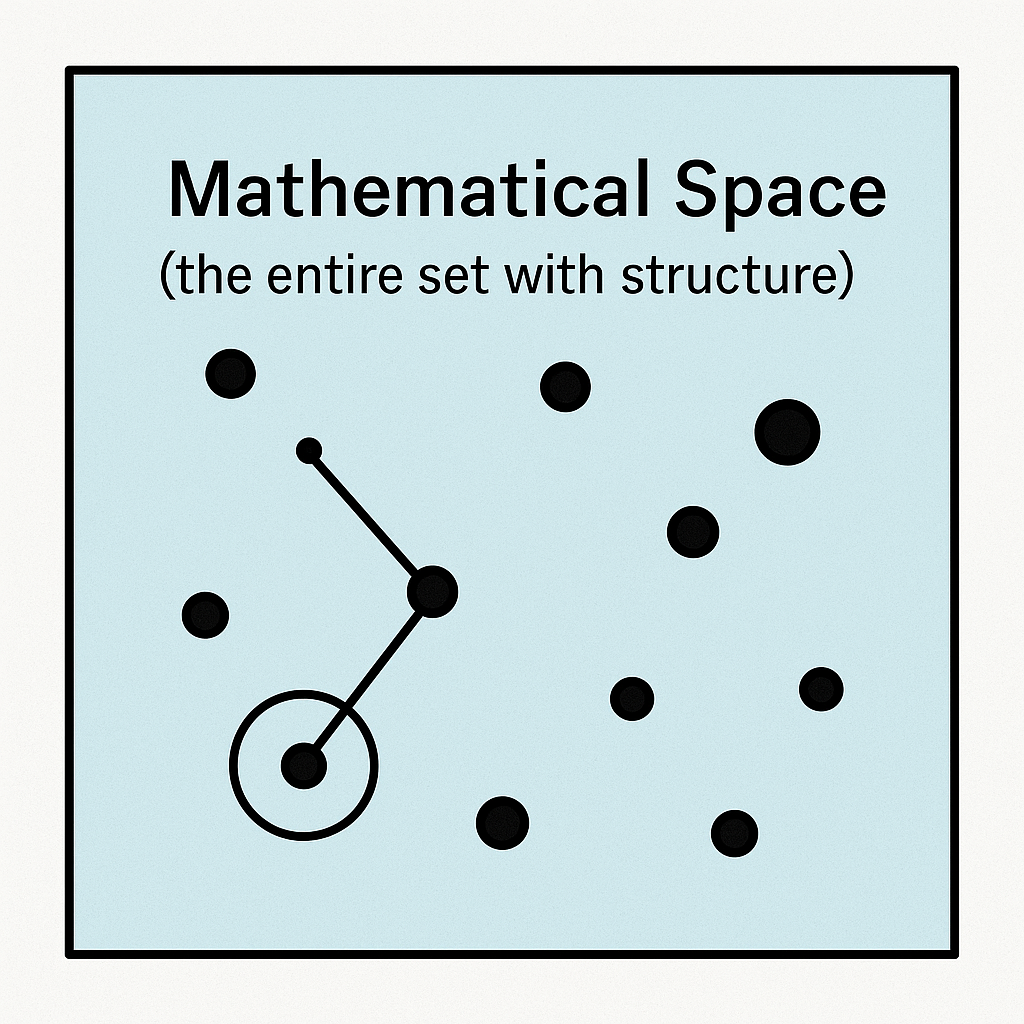
重要なのは、数学の空間が物質から独立に定義されるという点である。そこでは、人が存在できるか、移動できるかといった経験的条件は前提とされない。

数学において空間とは、議論や計算を行うためのよりどころであり、どのような構造を与えるかによって、距離を測ったり、近さを定義したり、連続的な変化を扱ったりすることが可能になる。

不整合の所在

ここまでを踏まえると、建築と数学における空間の不整合は、単なる言葉の混乱ではないことが分かる。
両者は同じ語を用いながら、中心に据えているものが異なっている。

建築において空間が中心に据えるのは、人の経験・行為・滞在である。
一方、数学において空間が中心に据えるのは、距離・近傍・連続性などの構造である。

建築の空間は、経験を成立させるために物質に依存する。一方、数学の空間は、構造を扱うために物質から切り離される。
たとえば、建築において歴史的に曲面形状を表現してきたNURBSの理論的背景には、数学的な空間がある。⁵曲面形状を俎上に載せて建築空間について議論する場面では、両者の文脈を把握しておく必要がある。

不整合をどう読むか

重要なのは、どちらの用法が正しいかを決めることではなく、空間という語が分野ごとに異なる役割を担っていることを理解することにある。

建築は、人の経験を組織するために空間という概念を用いる。
数学は、構造を扱うために空間という概念を用いる。

同じ語であっても、中心に据える対象が違えば、その意味も異なる。
ただし実務上は、両者の不整合が大きな問題として表面化しないことも多い。設計者と技術者の役割分担によって、両者の文脈が暗黙に切り分けられているからである。
そのうえで、数学の枠組みを導入することで建築の形状表現にさらなる発展を期待するのであれば、この整理には利用価値がある。

おわりに

本稿では、建築と幾何学における空間の違いを、最小限の前提で整理してきた。
不整合の原因は、専門性の高さそのものではなく、何を中心に据えて概念が構築されているかの違いにある。

Footnotes

1. 本稿では、建築設計の実務およびそれに接続する教育・技術的文脈を主な対象とし、哲学的空間論や数学そのものを網羅的に扱うことは目的としていない。 ↩

2. ここで述べる空間理解は、現代の建築設計実務において広く共有されている用法を念頭に置いたものであり、記号論的・制度的・都市論的な空間概念を代表するものではない。 ↩

3. このような理解は、現象学的建築論などにおいて論じられてきた立場と親和的であるが、本稿では特定の理論体系に依拠せず、実務的な理解の水準にとどめている。 ↩

4. 数学においては、距離を持たない空間や、より抽象的な構造によって定義される空間概念も存在する。本稿では、建築との対比を明確にするため、距離や近傍といった構造を持つ空間を代表例として取り上げている。 ↩

5. NURBSは、本稿で述べた両者の空間概念が実務上接続する代表的な事例として挙げており、理論的詳細そのものを論じる意図はない。 ↩